Mass transfer describes the transport of mass from one point to another and is one of the main pillars in the subject of Transport Phenomena. Mass transfer may take place in a single phase or over phase boundaries in multiphase systems. In the vast majority of engineering problems, mass transfer involves at least one fluid phase (gas or liquid), although it may also be described in solid-phase materials.
In many cases, the mass transfer of species takes place together with chemical reactions. This implies that flux of a chemical species does not have to be conserved in a volume element, since chemical species may be produced or consumed in such an element. The chemical reactions are sources or sinks in such flux balances.
The theory of mass transfer allows for the computation of mass flux in a system and the distribution of the mass of different species over time and space in such a system, also when chemical reactions are present. The purpose of such computations is to understand, and possibly design or control, such a system.
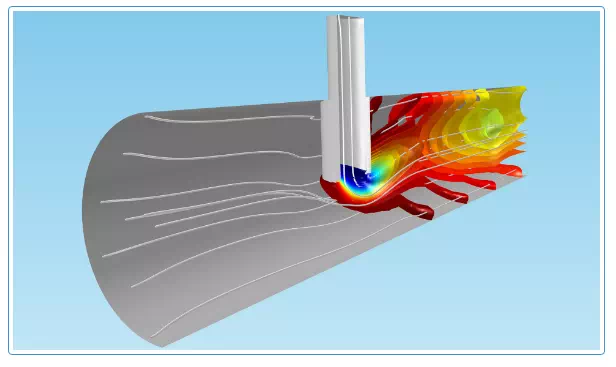
Transport and reactions in a reactor. The concentration isosurfaces reveal mass transfer through diffusion and convection. The flux through diffusion takes place perpendicular to the concentration isosurfaces, i.e., the reactions may cause a flux to the reaction site of the species that are consumed in the reaction. Convection creates a larger separation between the concentration isosurfaces and takes place along the streamlines of the fluid flow (in white), which in some places run along the isosurfaces, since convection tends to eliminate concentration gradients along its main direction.
Mathematical Description of Mass Transfer
The driving force, F, for mass transfer is created by gradients in the system potential, U:
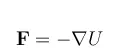
Gradients in chemical composition are usually responsible for this driving force. The driving force for transport over phase boundaries is generated by a deviation from equilibrium over such a phase boundary. Additional driving forces may contribute with a drift velocity, such as the forces created by migration, pressure, gravitational, and centrifugal forces.
The equation below shows the forces acting on a chemical species, per mole of atoms, ions, or molecules, due to gradients in chemical potential and electric fields (migration)
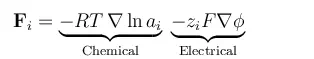
In these equations, R denotes the gas constant, T is the temperature, ai is the activity of each species, zi denotes the charge number of a species, F is the Faraday constant, and φ is the electric potential. The negative gradient of φ is the electric field. The activity can be understood as a thermodynamic measure of the chemical potential of the system, so that gradients in activity correspond to driving forces for chemical mass transport.
A simple chemical assumption is that the activity of a species i is given by its mole fraction, denoted as xi. This is exactly true for an ideal mixture.
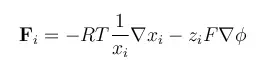
The forces on a species i are balanced by the friction in the interaction between this species and the other species in a mixture. The friction acting on a mole of i is proportional to the difference in mass velocity between i and each species j in the mixture, the mole fraction of each species j in a mixture, and the friction coefficient between i and j.
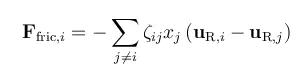
In this equation, ζij denotes the friction coefficient between species i and j, xj is the mole fraction of species j, and uR,i is the mass species velocity of species i relative to the mass average velocity of the whole mixture. Note that the mass velocities of each species in the equation above are given using the mass average velocity for the mixture as reference. A species that does not deviate from the velocity of the mixture (i.e., that does not diffuse or migrate, in this case), has a zero uR,i, when using the mixture velocity as reference.