Introduction

In the materials processing industry, size reduction or comminution is usually carried out in order to increase the surface area because, in most reactions involving solid particles, the rate of reactions is directly proportional to the area of contact with a second phase. Thus the rate of combustion of solid particles is proportional to the area presented to the gas, though a number of secondary factors may also be involved. For example, the free flow of gas may be impeded because of the higher resistance to flow of a bed of small particles. In leaching, not only is the rate of extraction increased by virtue of the increased area of contact between the solvent and the solid, but the distance the solvent has to penetrate into the particles in order to gain access to the more remote pockets of solute is also reduced. This factor is also important in the drying of porous solids, where reduction in size causes both an increase in area and a reduction in the distance the moisture must travel within the particles in order to reach the surface. In this case, the capillary forces acting on the moisture are also affected. There are a number of other reasons for carrying out size reduction. It may, for

example, be necessary to break a material into very small particles in order to separate two constituents, especially where one is dispersed in small isolated pockets. In addition, the properties of a material may be considerably influenced by the particle size and, for example, the chemical reactivity of fine particles is greater than that of coarse particles, and the colour and covering power of a pigment is considerably affected by the size of the particles. In addition, far more intimate mixing of solids can be achieved if the particle size is small.

Mechanism of size reduction

Whilst the mechanism of the process of size reduction is extremely complex, in recent years a number of attempts have been made at a more detailed analysis of the problem. If a single lump of material is subjected to a sudden impact, it will generally break so as to yield a few relatively large particles and a number of fine particles, with relatively few particles of intermediate size. If the energy in the blow is increased, the larger particles will be of a rather smaller size and more numerous and, whereas the number of fine particles will be appreciably increased, their size will not be much altered. It therefore appears that the size of the fine particles is closely connected with the internal structure of the material, and the size of the larger particles is more closely connected with the process by which the size reduction is effected. This effect is well illustrated by a series of experiments on the grinding of coal ina small mill, carried out by HEYWOOD(1). The results are shown in Figure 2.1, in which the distribution of particle size in the product is shown as a function of the number of Figure 2.1.

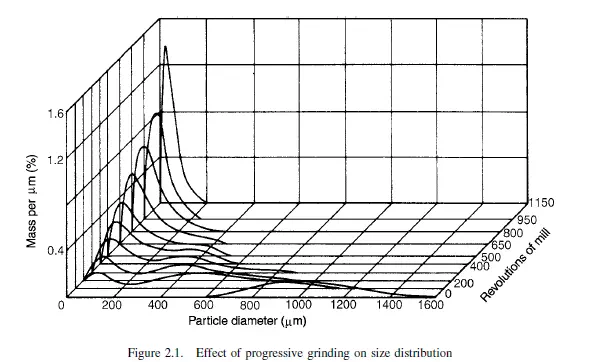
revolutions of the mill. The initial size distribution shows a single mode corresponding to a relatively coarse size, but as the degree of crushing is gradually increased this mode progressively decreases in magnitude and a second mode develops at a particular size. This process continues until the first mode has completely disappeared. Here the second mode is characteristic of the material and is known as the persistent mode, and the first is known as the transitory mode. There appears to be a grind limit for a particular material  and machine. After some time there seems to be little change in particle size if grinding  is continued, though the particles may show some irreversible plastic deformation which results in a change in shape rather than in size. The energy required to effect size reduction is related to the internal structure of

the material and the process consists of two parts, first opening up any small fissures which are already present, and secondly forming new surface. A material such as coal

contains a number of small cracks and tends first to break along these, and therefore the large pieces are broken up more readily than the small ones. Since a very much

greater increase in surface results from crushing a given quantity of fine as opposed to coarse material, fine grinding requires very much more power. Very fine grinding can be impeded by the tendency of some relatively soft materials, including gypsum and some limestones, to form aggregates. These are groups of relatively weakly adhering particles held together by cohesive and van der Waals forces. Materials, such as quartz and clinker, form agglomerates in which the forces causing adhesion may be chemical in nature, and the bonds are then very much stronger. In considering energy utilisation, size reduction is a very inefficient process and only between 0.1 and 2.0 per cent of the energy supplied to the machine appears as increased surface energy in the solids. The efficiency of the process is very much influenced by the manner in which the load is applied and its magnitude. In addition the nature of the force exerted is also very important depending, for example, on whether it is predominantly

a compressive, an impact or a shearing force. If the applied force is insufficient for the elastic limit to be exceeded, and the material is compressed, energy is stored in the

particle. When the load is removed, the particle expands again to its original condition without doing useful work. The energy appears as heat and no size reduction is effected. A somewhat greater force will cause the particle to fracture, however, and in order to obtain the most effective utilisation of energy the force should be only slightly in excess of the crushing strength of the material. The surface of the particles will generally be of a very irregular nature so that the force is initially taken on the high spots, with the result that very high stresses and temperatures may be set up locally in the material. As soon as a small amount of breakdown of material takes place, the point of application of the force alters. BEMROSE and BRIDGEWATER(2) and HESS and SCHO¨ NERT(3) have studied the breakage of single particles. All large lumps of material contain cracks and size reduction occurs as a result of crack propagation that occurs above a critical parameter, F, where:

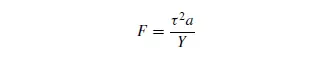
where: a = crack length,

τ = stress, and

Y = Young’s modulus.

HESS(3) suggests that at lower values of F, elastic deformation occurs without fracture and the energy input is completely ineffective in achieving size reduction. Fundamental studies of the application of fracture mechanics to particle size reduction have been carried out, by SCHO¨ NERT(4). In essence, an energy balance is applied to the process of crack extension within a particle by equating the loss of energy from the strain field within the particle to the increase in surface energy when the crack propagates. Because of plastic deformation near the tip of the crack, however, the energy requirement is at least ten times greater and, in addition kinetic energy is associated with the sudden acceleration of material as the crack passes through it. Orders of magnitude of the surface fracture energy per unit volume are:

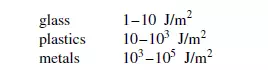
All of these values are several orders of magnitude higher than the thermodynamic surface energy which is about 10−1 J/m2. Where a crack is initially present in a material, the stresses near the tip of the crack are considerably greater than those in the bulk of the material. Calculation of the actual value is well nigh impossible as the crack surfaces are usually steeply curved and rough. The presence of a crack modifies the stress field in i√ts immediate location, with the increase in energy being approximately proportional to (a/l) where a is the crack length and l is the distance from the crack tip. Changes in crack length are accompanied by modifications in stress distribution in the surrounding material and hence in its energy content. During the course of the size reduction processes, much energy is expended in causing plastic deformation and this energy may be regarded as a waste as it does not result in fracture. Only part of it is retained in the system as a result of elastic recovery. It is not possible, however, to achieve the stress levels necessary for fracture to occur without first passing through the condition of plastic deformation and, in this sense, this must be regarded as a necessary state which must be achieved before fracture can possibly occur. The nature of the flaws in the particles changes with their size. If, as is customary,

fine particles are produced by crushing large particles, the weakest flaws will be progressively eliminated as the size is reduced, and thus small particles tend to be stronger

and to require more energy for fracture to occur. In addition, as the capacity of the particle for storing energy is proportional to its volume (∝ d3) and the energy requirement for propagating geometrically similar cracks is proportional to the surface area (∝ d2), the energy available per unit crack area increases linearly with particle size (d). Thus, breakage will occur at lower levels of stress in large particles. This is illustrated in Figure 2.2 which shows the results of experimental measurements of the compressive strengths for shearing two types of glass. It may be noted from Figure 2.2 that, for quartz glass, the compressive strength of 2 μm particles is about three times that of 100 μm particles. The exact method by which fracture occurs is not known, although it is suggested by PIRET(5) that the compressive force produces small flaws in the material. If the energy concentration exceeds a certain critical value, these flaws will grow rapidly and will generally branch, and the particles will break up. The probability of fracture of a particle

in an assembly of particles increases with the number of contact points, up to a number of around ten, although the probability then decreases for further increase in number. The rate of application of the force is important because there is generally a time lag between attainment of maximum load and fracture. Thus, a rather smaller force will cause fracture provided it is maintained for a sufficient time. This is a phenomenon similar to the ignition lag which is obtained with a combustible gas–oxidant mixture. Here the interval between introducing the ignition source and the occurrence of ignition is a function of the temperature of the source, and when it is near the minimum ignition temperature delays of several seconds may be encountered. The greater the rate at which the load is applied, the less effectively is the energy utilised and the higher is the proportion of fine material which is produced. If the particle shows any viscoelastic behaviour, a high rate of application  of the force is needed for fracture to occur. The efficiency of utilisation of energy as supplied by a falling mass has been compared with that of energy applied slowly by means of hydraulic pressure. Up to three or four times more surface can be produced per unit of energy if it is applied by the latter method. PIRET(5) suggests that there is a close similarity between the crushing operation and a chemical reaction. In both cases a critical energy level must be exceeded before the process will start, and in both cases time is an important variable. The method of application of the force to the particles may affect the breakage pattern. PRASHER(6) suggests that four basic patterns may be identified, though it is sometimes difficult to identify the dominant mode in any given machine. The four basic patterns are:

a)    Impact —particle concussion by a single rigid force.

b)    Compression—particle disintegration by two rigid forces.

c)     Shear —produced by a fluid or by particle–particle interaction.

d)    Attrition —arising from particles scraping against one another or against a rigid surface.

Energy for size reduction

Energy requirements

Although it is impossible to estimate accurately the amount of energy required in order to effect a size reduction of a given material, a number of empirical laws have been

proposed. The two earliest laws are due to KICK(7) and VON RITTINGER(8), and a third law due to BOND(9,10) has also been proposed. These three laws may all be derived from the basic differential equation:

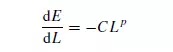
which states that the energy dE required to effect a small change dL in the size of unit mass of material is a simple power function of the size. If p = −2, then integration gives:

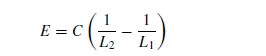
Writing C = KRfc, where fc is the crushing strength of the material, then Rittinger’s law  first postulated in 1867, is obtained as:

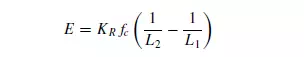
Since the surface of unit mass of material is proportional to 1/L, the interpretation of this law is that the energy required for size reduction is directly proportional to the increase in surface.

If p = −1, then:

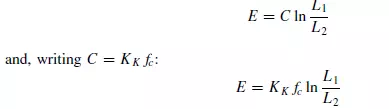
which is known as Kick’s law. This supposes that the energy required is directly related to the reduction ratio L1/L2 which means that the energy required to crush a given amount of material from a 50 mm to a 25 mm size is the same as that required to reduce the size from 12 mm to 6 mm. In equations 2.3 and 2.4, KR and KK are known respectively as Rittinger’s constant and Kick’s constant. It may be noted that neither of these constants is dimensionless. Neither of these two laws permits an accurate calculation of the energy requirements. Rittinger’s law is applicable mainly to that part of the process where new surface is being created and holds most accurately for fine grinding where the increase in surface per unit mass of material is large. Kick’s law, more closely relates to the energy required to effect elastic deformation before fracture occurs, and is more accurate than Rittinger’s law for coarse crushing where the amount of surface produced is considerably less. Bond has suggested a law intermediate between Rittinger’s and Kick’s laws, by putting p = −3/2 in equation 2.1. Thus:

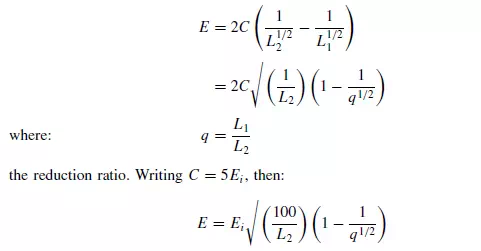
Bond terms Ei the work index, and expresses it as the amount of energy required to reduce unit mass of material from an infinite particle size to a size L2 of 100 μm, that

is q =∞. The size of material is taken as the size of the square hole through which 80 per cent of the material will pass. Expressions for the work index are given in the

original papers(8,9) for various types of materials and various forms of size reduction equipment. AUSTIN and KLIMPEL(11) have reviewed these three laws and their applicability, and CUTTING(12) has described laboratory work to assess grindability using rod mill tests.

Example

A material is crushed in a Blake jaw crusher such that the average size of particle is reduced from 50 mm to 10 mm with the consumption of energy of 13.0 kW/(kg/s). What would be the consumption of energy needed to crush the same material of average size 75 mm to an average size of 25 mm:

a)    assuming Rittinger’s law applies?

b)    assuming Kick’s law applies?

Which of these results would be regarded as being more reliable and why?

Solution

a) Rittinger’s law.

This is given by: E = KRfc[(1/L2) − (1/L1)] (equation 2.3)

Thus: 13.0 KRfc[(1/10) − (1/50)]

and: KRfc = (13.0 × 50/4) = 162.5 kW/(kg mm)

Thus the energy required to crush 75 mm material to 25 mm is: E = 162.5[(1/25) − (1/75)] = 4.33 kJ/kg

b) Kick’s law.

This is given by: E = KKfc ln(L1/L2) (equation 2.4)

Thus: 13.0 = KKfc ln(50/10)

and: KKfc = (13.0/1.609) = 8/08 kW/(kg/s)

Thus the energy required to crush 75 mm material to 25 mm is given by: E = 8.08 ln(75/25) = 8.88 kJ/kg

The size range involved by be considered as that for coarse crushing and, because Kick’s law more closely relates the energy required to effect elastic deformation before fracture occurs, this would be taken as given the more reliable result.