General characteristics

The properties of solids in bulk are a function of the properties of the individual particles including their shapes and sizes and size distribution, and of the way in which the particles interact with one another. By the very nature of a particulate material, it is always interspersed with a fluid, generally air, and the interaction between the fluid and the particles may have a considerable effect on the behaviour of the bulk material. Particulate solids present considerably greater problems than fluids in storage, in removal at a controlled rate from storage, and when introduced into vessels or reactors where they become involved in a process. Although there has recently been a considerable amount of work carried out on the properties and behaviour of solids in bulk, there is still a considerable lack of understanding of all the factors determining their behaviour. One of the most important characteristics of any particulate mass is its voidage, the fraction of the total volume which is made up of the free space between the particles and is filled with fluid. Clearly, a low voidage corresponds to a high density of packing of the particles. The way in which the particles pack depends not only on their physical properties, including shape and size distribution, but also on the way in which the particulate mass has been introduced to its particular location. In general, isometric particles, which have approximately the same linear dimension in each of the three principal directions, will pack more densely than long thin particles or plates. The more rapidly material is poured on to a surface or into a vessel, the more densely will it pack. If it is then subjected to vibration, further consolidation may occur. The packing density or voidage is important in that it determines the bulk density of the material, and hence the volume taken up by a given mass: It affects the tendency for agglomeration of the particles, and it critically influences the resistance which the material offers to the percolation of fluid through it—as, for example, in filtration as discussed in Chapter 7.

Agglomeration

Because it is necessary in processing plant to transfer material from storage to process, it is important to know how the particulate material will flow. If a significant amount

of the material is in the form of particles smaller than 10 μm or if the particles deviate substantially from isometric form, it may be inferred that the flow characteristics will be poor. If the particles tend to agglomerate, poor flow properties may again be expected. Agglomeration arises from interaction between particles, as a result of which they adhere to one another to form clusters. The main mechanisms giving rise to agglomeration are:

1)     Mechanical interlocking. This can occur particularly if the particles are long and thin in shape, in which case large masses may become completely interlocked.

2)     Surface attraction. Surface forces, including van der Waals’ forces, may give rise to substantial bonds between particles, particularly where particles are very fine (<10 μm), with the result that their surface per unit volume is high. In general, freshly formed surface, such as that resulting from particle fracture, gives rise to high        surface forces.

3)     Plastic welding. When irregular particles are in contact, the forces between the particles will be borne on extremely small surfaces and the very high pressures

developed may give rise to plastic welding.

4)     Electrostatic attraction. Particles may become charged as they are fed into equipment and significant electrostatic charges may be built up, particularly on fine solids.

5)     Effect of moisture. Moisture may have two effects. Firstly, it will tend to collect near the points of contact between particles and give rise to surface tension effects.

Secondly, it may dissolve a little of the solid, which then acts as a bonding agent on subsequent evaporation.

6)     Temperature fluctuations give rise to changes in particle structure and to greater cohesiveness.

Because interparticle forces in very fine powders make them very difficult to handle, the effective particle size is frequently increased by agglomeration. This topic is discussed in Section 2.4 on particle size enlargement in Chapter 2.

Resistance to shear and tensile forces

A particulate mass may offer a significant resistance to both shear and tensile forces, and this is specially marked when there is a significant amount of agglomeration. Even in non-agglomerating powders there is some resistance to relative movement between the particles and it is always necessary for the bed to dilate, that is for the particles to move apart, to some extent before internal movement can take place. The greater the density of packing, the higher will be this resistance to shear and tension.

The resistance of a particulate mass to shear may be measured in a shear cell such as that described by JENIKE et al.(11,12) The powder is contained in a shallow cylindrical

cell (with a vertical axis) which is split horizontally. The lower half of the cell is fixed and the upper half is subjected to a shear force which is applied slowly and continuously measured. The shearing is carried out for a range of normal loads, and the relationship between shear force and normal force is measured to give the shear strength at different degrees of compaction. A method of measuring tensile strength has been developed by ASHTON et al.(13) who also used a cylindrical cell split diametrically. One half of the cell is fixed and the other, which is movable, is connected to a spring, the other end of which is driven at a slow constant speed. A slowly increasing force is thus exerted on the powder compact and the point at which failure occurs determines the tensile strength; this has been shown to depend on the degree of compaction of the powder. The magnitude of the shear and tensile strength of the powder has a considerable effect on the way in which the powder will flow, and particularly on the way in which it will discharge from a storage hopper through an outlet nozzle.

Angles of repose and of friction

A rapid method of assessing the behaviour of a particulate mass is to measure its angle of repose. If solid is poured from a nozzle on to a plane surface, it will form an approximately conical heap and the angle between the sloping side of the cone and the horizontal is the angle of repose. When this is determined in this manner it is sometimes referred to as the dynamic angle of repose or the poured angle. In practice, the heap will not be exactly conical and there will be irregularities in the sloping surface. In addition, there will be a tendency for large particles to roll down from the top and collect at the base, thus giving a greater angle at the top and a smaller angle at the bottom. The angle of repose may also be measured using a plane sheet to which is stuck a layer of particles from the powder. Loose powder is then poured on to the sheet which is then tilted until the powder slides. The angle of slide is known as the static angle of repose or the drained angle. Angles of repose vary from about 20◦ with free-flowing solids, to about 60◦ with solids with poor flow characteristics. In extreme cases of highly agglomerated solids, angles of repose up to nearly 90◦ can be obtained. Generally, material which contains no particles smaller than 100 μm has a low angle of repose. Powders with low angles of repose tend to pack rapidly to give a high packing density almost immediately. If the angle of reposeis large, a loose structure is formed initially and the material subsequently consolidates if

subjected to vibration. An angle which is similar to the static angle of repose is the angle of slide which is measured in the same manner as the drained angle except that the surface is smooth and is not coated with a layer of particles.

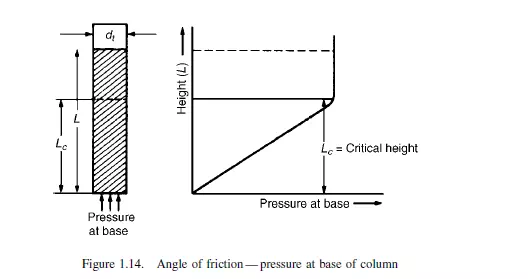
A measure of the frictional forces within the particulate mass is the angle of friction. This can be measured in a number of ways, two of which are described. In the first, the

powder is contained in a two-dimensional bed, as shown in Figure 1.12 with transparent walls and is allowed to flow out through a slot in the centre of the base. It is found

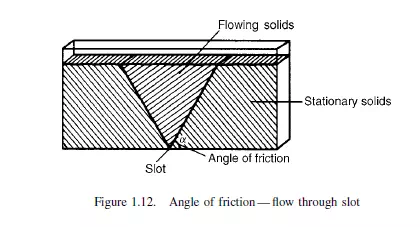
that a triangular wedge of material in the centre flows out leaving stationary material at the outside. The angle between the cleavage separating stationary and flowing material and the horizontal is the angle of friction. A simple alternative method of measuring the angle of friction, as described by ZENZ(14), employs a vertical tube, open at the top, with a loosely fitting piston in the base as shown in Figure 1.13. With small quantities of solid in the tube, the piston will freely move upwards, but when a certain critical amount is exceeded no force, however large, will force the solids upwards in the tube. With the largest movable core of solids in the tube, the ratio of its length to diameter is the tangent of the angle of friction.

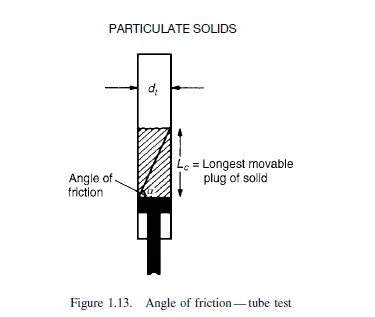
The angle of friction is important in its effect on the design of bins and hoppers. If the pressure at the base of a column of solids is measured as a function of depth, it is found

to increase approximately linearly with height up to a certain critical point beyond which it remains constant. A typical curve is shown in Figure 1.14. The point of discontinuity on the curve is given by:

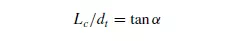
s