For most elementary reactions, the rearrangement of atoms in going from reactants to products via a transition state (see, for example, Figure 1.1.1) proceeds through the movements of atomic nuclei that experience a potential energy field that is generated by the rapid motions of the electrons in the system. On this potential energy surface there will be a path of minimum energy expenditure for the reaction to proceed from reactants to products (reaction coordinate). The low energy positions of reactants and products on the potential energy surface will be separated by a higher energy region. The highest energy along the minimum energy pathway in going from reactants to products defines the transition state. As stated in Chapter I, the transition state is not a reaction intermediate but rather a high energy configuration of a system in transit from one state to another.

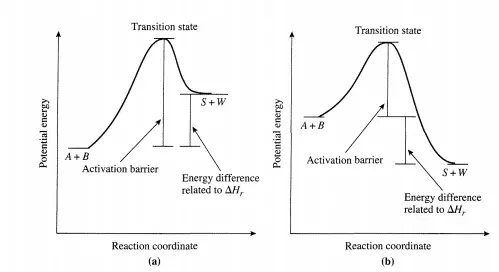
The difference in energies of the reactants and products is related to the heat of reaction-a thermodynamic quantity. Figure 2.3.1 shows potential energy profiles for endothermic and exothermic elementary reactions. Transition-state theory is used to calculate an elementary reaction that conforms to the energetic picture illustrated in Figure 2.3.1. How this is done is described next.

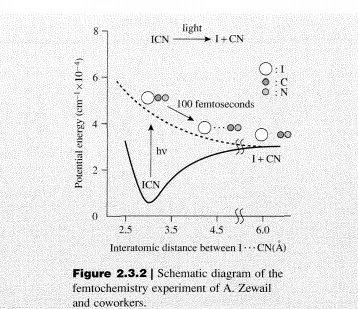
Consider again the reaction given by Equation (2.2.2). At thermodynamic equilibrium, Equation (2.2.3) is satisfied. In the equilibrated system, there must also exist an equilibrium concentration of transition states: CTS’ The rates of the forward and the reverse reactions are equal, implying that there is an equivalent number of species traversing the activation barrier from either the reactant side or the product side. Thus,

and LlGt is the change in the standard Gibbs function for the reaction given in Equation (2.3.3) and LlHt and LlSt are the corresponding changes in standard enthalpy and entropy, respectively. The subscript 0 is used to denote the standard state while the superscript =1= denotes quantities pertaining to the transition state. By combining Equations (2.3.5) and (2.3.4), CTS can be written as:

This is the general equation of transition-state theory in its thermodynamic form.