“During the latter part of the 19th century, physicists were justly proud of the apparent completeness of their subject. Newton’s laws and the electromagnetic wave theory of Maxwell had successfully explained most of the phenomena they were interested in. As experiments were able to go to lower temperatures and to both shorter and longer wavelengths of radiation, problems arose which showed that the classical laws [of the motion of matter] did not explain phenomena on the atomic or molecular level.”[1] In a effort to explain these decrepencies quantum mechanics was born.

Quantum mechanics mathematically describes the motion of electrons via a simple postulate. The postulate states that energy can only be transferred from the particle’s surroundings to a particle in specific quantities. It turns out that many useful properties of atoms and molecules can be predicted using quantum mechanical calculations. For example, heats of reaction, rate constants, molecular vibrational frequencies, and many other physical properties can be calculated using quantum mechanical methods, without any prior knowledge from experiments. Just as this intrinsic reaction coordinate was calculated using the Spartan program:

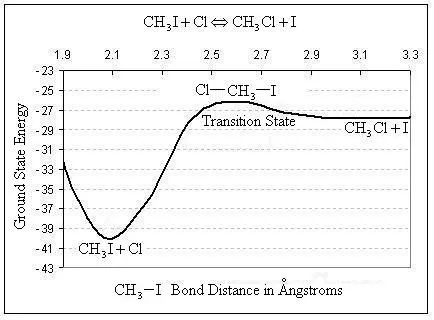
A brief background on quantum mechanical calculations is provided here,  Fortunately, computational chemistry software has advanced to the point that we can perform calculations based on quantum chemistry without having to work through all the details ourselves. We will explore the use of some of this software in the present exercise.

What is statistical mechanics?

Statistical mechanics is defined as the study of the properties of a macroscopic system as predicted by the statistical behavior of its constituent microscopic particles. Statistical mechanics was developed by many different historical scientists over the last century. Statistical mechanics is used to calculate thermodynamic quantities from microscopic properties of a system. Because of its wide reaching applications we will only focus on what we will be using within this web module. First we will discuss some of the key aspects of statistical mechanics that will be applied in this web module. First, partition functions are mathematical functions that take into account the many ways that energy can be partitioned (i.e, distributed) in a system. The four partition functions that we (the programs) will be dealing with are vibrational, translational, rotational, and electronic partition functions. These four partition functions describe the four different ways that a quantity, such as energy, can be distributed within a microscopic system. With these partition functions, one can calculate the enthalpy, entropy, heat capacity, and zero point energy. For a more in-depth discussion of statistical mechanics select one of the document types .

What is transition state theory?

Transition state theory basically states that in a chemical reaction the reactants proceed through a high energy transition state before forming the products of the reaction. Basically, several quantities such as the activation energy and the preexponential factor can be calculated using thermodynamic mathematical relationships and the thermodynamic quantities of the transition state. Transition state theory relies upon many mathematical and theoretical foundations fet forth by statistical mechanics and quantum mechanics. For a in-depth background on transition state theory and an example of how quantum mechanics, statistical mechanics, and transition state theory are coupled select one of the document types (HTML, PDF).

What are the applications to chemical engineering?

Quantum mechanics, statistical mechanics, and transition state theory can be applied to many chemical engineering problems, and are used for applications ranging from the manufacture of large-volume petrochemicals to characterization of enzyme-substrate interactions to analysis of thin film deposition on semiconductor chips. For chemical engineers, molecular modeling calculations are most useful in determining kinetic and thermodynamic properties of a reaction system. The next generation of chemical engineers will rely heavily on molecular modeling and quantum mechanical calculations to design reactions to produce pharmaceuticals, industrial chemicals, and complex molecules. Here’s a list of what we’ll be using these sorts of calculations to do:

Quantities that can be calculated using Quantum Mechanical Software

·         Enthalpy of each state

·         Gibbs free energy for each state

·         Entropy for each state

·         Heat of reaction

·         Activation energy

·         Preexponential factor

·         Rate constant as a function of temperature

·         Total bond energy, heat of formation, or total energy of the molecule

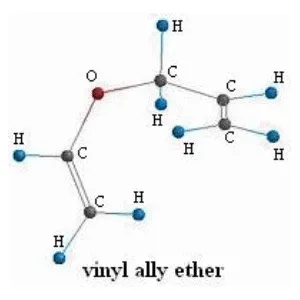
Let’s take a look at a real example

Vinyl Allyl Ether4-Pentenal

Figure 2.

If we didn’t have a computer or quantum mechanics what would we do to design chemical reaction systems?

• As a first option, head to the library to see whether any published data is available for this reaction; however, this is not available for many reaction systems.
• Head to the laboratory to do a bunch of experiments
  • Use a calorimeter to calculate the heat of formation, heat of reaction, and heat capacity
  • Use a bench-scale differential reactor or batch reactor to gain data such that the activation energy and preexponential factor could be calculated
• Spend a lot of time and money on experiments, remember that “six weeks in the lab may save you a hour in the library”-George Quanderer Dow Chemical.

Because we do have computers and quantum mechanics, we will proceed like this:

• Start to think about the reaction on a molecular level
• Try to postulate a logical mechanism for the reaction
• Use a computational chemistry software package such as Cerius2, Spartan, or Gaussian to calculate thermodynamic properties of reactants, transition state, and products
• Use these properties to calculate the activation energy and the preexponential factor

Presently:

Computational chemistry has not yet advanced to the point where large-scale plants can be designed solely on a theoretical basis. However, the calculated quantities can help you:

1. Decide if a reaction system is even feasible for further development, before you spend a lot of money and time doing experiments
2. Determine whether experimental results (which aren’t always correct and reproducible!) are consistent with what you expect for the system at hand
3. Help identify an improved process (e.g., a new catalyst)

What do you think the transition state would look like?

If we take a close look at the reaction above we can see that three things happen:

• A carbon-oxygen bond is broken
• A carbon-carbon bond is formed
• A carbon-oxygen double bond is formed

Since we start and end with the same atoms in the molecule the reaction must be intramolecular. So if we just bring the two free ends of the molecule together and “push” some electrons around like this:

Figure 3.

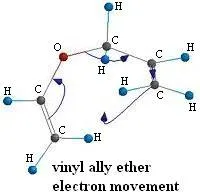
The arrows that you see in figure 3 represent the movement of the electrons as the molecule transitions from the reactant to the transition state.

And thus the transition state would be:

Figure 4.

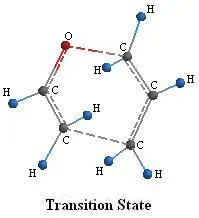
In figure 4 the dashed lines represent the bonds being formed and broken in the transition state.

Now on the molecular level the reaction is:

Great! That is all we need to start using the computational chemistry software.

Using the software

Upon dismantling the reaction into a logical mechanism we can simply draw each structure in the software and calculate the needed values. We’ll go through the results of this process to provide an overview of how we’ll proceed, then go through a step-by-step example.

Step 1: reactant

After drawing the reactant structure in the software we run a basic geometry optimization with a frequency calculation to obtain the thermodynamic quantities: entropy, enthalpy, zero point energy, and ground state energy. The data output at STP in tabular form for vinyl allyl ether is:

Variable	Definition	Value	Units
ZPE ( T = 0 K )	Zero point Energy	+74.29	kcal/mol
GSE ( T = 298.15 K )	Ground State Energy	-169744.25	kcal/mol
H ( T = 298.15 K )	Enthalpy	+78.67	kcal/mol
S ( T = 298.15 K )	Entropy	+82.40	cal/mol K
G = H – T*S	Gibbs Free Energy	+54.10	kcal/mol

Step 2: transition state

After drawing a plausible configuration of the transition state we run a transition state search and are able to find the true transition state. Which is characterized by an imaginary frequency in the direction of the reaction and also obtain thermodynamic quantities. The data output at STP in tabular form for the transition state is:

Variable	Definition	Value	Units
ZPE ( T = 0 K )	Zero point Energy	+73.46	kcal/mol
GSE (T)	Ground State Energy	-169717.04	kcal/mol
H (T)	Enthalpy	+77.21	kcal/mol
S (T)	Entropy	+75.73	cal/mol K
G = H – T*S	Gibbs Free Energy	+54.63	kcal/mol

Step 3: product

To obtain the thermodynamic quantities for the product structure we just repeat step 1 using the product structure instead of the reactant. The data output at STP in tabular form for 4-pentenal is:

Variable	Definition	Value	Units
ZPE ( T = 0 K )	Zero point Energy	+74.28	kcal/mol
GSE (T)	Ground State Energy	-169762.87	kcal/mol
H (T)	Enthalpy	+78.66	kcal/mol
S (T)	Entropy	+82.74	cal/mol K
G = H – T*S	Gibbs Free Energy	+53.99	kcal/mol

Step 4: results

With these values we can calculate the heat of reaction, the change in entropy, the change in Gibbs free energy, estimate the activation energy, and calculate the preexponential factor.

The heat of reaction for a general reaction such as:

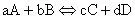 (8)

is:

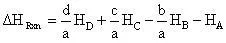 (9)

because we are dealing with a unimolecular reaction the general reaction equation reduces to:

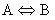 (10)

and thus the heat of reaction would be:

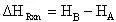 (11)

We can use this equation as is if the program we are using gives us a heat of formation of the reactant, transition state, and product, but if the program does not, then we will have to resort to a slightly modified version of the above heat of reaction equation. This modification does not mean that we are calculating something different it just means that we are calculating the heat of reaction differently.

Some programs do not calculate the heat of formation but instead quantum mechanically calculate what we will call the ground state energy (GSE). This GSE is usually calculated in two different ways which only differ from each other in what the programs define as zero energy. Spartan, for example, defines zero energy of the system as the energy associated with all of the nuclei and electrons an infinite distance from each other. In other words, zero energy is when there are no interactions between any subatomic particles in the system. Thus Spartan calculates the amount of energy needed or released when all of the subatomic particles are brought together to form the molecule or molecules. These calculations usually are characterized by a large negative GSEs. As an example you could think of disassociating all of the subatomic particles of the vinyl allyl ether molecule to an infinite distance from each other and realize that one would need a lot of energy to do that, thus when you do just the opposite a lot of energy will be given off hence the large negative GSE. An alternate way of calculating the GSE is to reference molecular or atomic fragments as zero energy (just as Cerius2 does) and calculate the energy needed or released by bringing the fragments together. Atomic fragments are defined usually as an atom in its natural bonding state (e.g., hydrogen with one proton and one electron or carbon with four sp3 hybridized orbitals with one electron residing in each hybrid orbital).

Another little speed bump is that the GSE does not take into account the energy contained in the vibration, rotation, and translation of the molecule. This energy can be accounted for by using statistical mechanics (the program will do this). In statistical mechanics one can use the molecular frequencies calculated by the program and calculate thermodynamic quantities. We will be using the statistical mechanically calculated enthalpy and entropy, this enthalpy and entropy only takes into account the energy in the vibrations, rotations, and translations so it is not representative of the total energy of the molecule, because a large portion of the energy in a molecule is contained in its bonds and physical conformation. That is why we must take the sum of the GSE and the statistical mechanically calculated enthalpy to arrive at a closer approximation of the true energy of the molecule. With that said we will now define a slightly modified version of the heat of reaction equation:

The enthalpy of a species will be defined as:

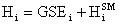 (12)

where the superscript SM denotes the statistical mechanically calculated enthalpy. Substituting this definition into the usual definition of the heat of reaction we arrive at:

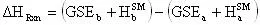 (13)

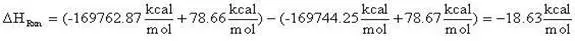
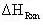 = -18.63 kcal/mol

The entropy can be calculated in the normal fashion by taking the difference of the products and reactants entropy:

 (14)

From the tabularized data above:

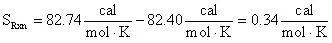
Therefore:

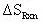= 0.34 cal/mol

Since the heat of reaction is not of the usual form the calculation of the Gibbs free energy will need to be calculated by the following method:

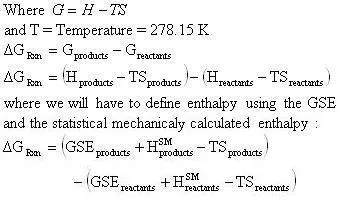
From the tabularized values above:

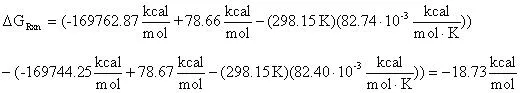
Therefore:

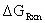 = -18.73 kcal/mol

The equilibrium constant can be calculated using the Gibbs free energy change of the reaction:

 (15)

From the tabularized values above:

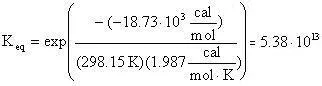
Therefore:

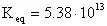
The activation energy of this reaction can be calculated by:

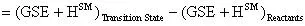
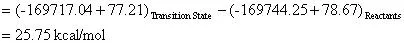
The preexponential factor (A) can be calculated using a bit of transition state theory that will be explained more in depth in the next example. For now the equation to calculate the preexponential factor is:

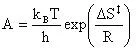 (16)

First, to calculate the change of entropy between the transition state and the reactants:

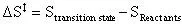 (17)

With values from the tables above:

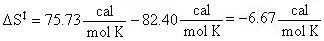
Therefore:

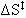 = -6.67 cal/mol K

Now the preexponential is calculated as:

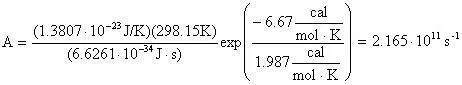
Which equals 2.165E11 reciprical seconds